Los grandes avances en la informática y la comunicación de los últimos años hacen prever una revolución que está sólo en sus inicios. Las nuevas tecnologías se utilizan para comunicarse, como herramienta de trabajo y también como instrumento de ocio. Aparecen en todas las parcelas de la vida actual, desde la investigación científica hasta el mundo de la empresa, pasando por la enseñanza. En esta última, se puede considerar que el uso de estos avances favorece el desarrollo de capacidades intelectuales y la adquisición de destrezas por parte del alumno, mediante una nueva forma de organizar, distribuir, representar y codificar la realidad.
Muchas son las ventajas que el desarrollo tecnológico ofrece a los docentes, así como algunos inconvenientes que pueden convertirlo en un arma de doble filo si no se hace un uso correcto del mismo. Corresponde al profesor/instructor determinar los límites que han de ser impuestos en su uso, así como extraerle el mayor rendimiento en términos pedagógicos.
De entre las ventajas, señalemos que proporciona medios con los que desarrollar nuestra labor de manera más eficiente, ya que permite la sustitución de técnicas que han quedado obsoletas. Además, hace posible el desarrollo de programas que facilitan la asimilación de los conceptos, eliminando el papel estático que la masificación ha otorgado al alumno. En otras palabras, las nuevas tecnologías posibilitan la interacción, un factor esencial en el proceso de enseñanza–aprendizaje.
Las materias del currículo que más se benefician de las nuevas tecnologías son, sin duda alguna, las asignaturas científicas y, de entre ellas, la Matemática. De hecho, la propia Matemática impulsa el desarrollo de software, a la vez que saca provecho de la mayor potencia de cálculo de las nuevas máquinas. A pesar de ello, la docencia en las asignaturas básicas de matemáticas parecía haber resistido a la invasión tecnológica. La razón esgrimida por muchos para justificar este inmovilismo es que la abstracción de los conceptos matemáticos sólo podía plasmarse con lápiz y papel, obviando todo tipo de dificultades computacionales. Pero no falta quien objeta que, puesto que en la práctica la calculadora o el ordenador terminan siendo indispensables, no está de más que los estudiantes se familiaricen cuanto antes con su uso. A este argumento se ha unido la aparición de una nueva herramienta informática para el trabajo con las matemáticas: los manipuladores simbólicos.
En el mercado existe una amplia oferta de este tipo de programas, comenzando por DERIVE (usado habitualmente en los Bachilleratos), MATLAB, MAPLE, MATHEMATICA, MuPAD, etc. Si bien cada uno de ellos presenta particularidades propias en el uso avanzado, todos ellos poseen un esquema similar de manejo básico.
Aunque a primera vista un manipulador simbólico puede interpretarse como una calculadora muy potente, en realidad se trata de un laboratorio matemático completo con posibilidades de edición y presentación visual que permiten darle la apariencia de un escrito matemático clásico. Los manipuladores actuales son de fácil manejo y poseen una sintaxis muy intuitiva, por lo que el estudiante puede comenzar el trabajo con ellos sin necesidad de consumir mucho tiempo en su aprendizaje. Por otra parte, el hecho de que se compilen y ejecuten línea a línea, si así se desea, permite una interacción continua sobre los datos introducidos que dinamiza los cálculos.
En las enseñanzas técnicas, donde una componente fundamental está constituida por los cálculos numéricos, el ordenador se convierte en una de las herramientas más potentes. Sin embargo, creemos que la formación de un técnico superior no debe restringirse al uso del software, sino que la diferencia entre un simple operario y un ingeniero debe estar precisamente en la capacidad de interacción con él. Es imprescindible, por tanto, un conocimiento de los métodos utilizados y no sólo del programa informático.
La necesidad de una formación básica en cálculo numérico se justifica por la ingente cantidad de problemas que no pueden ser resueltos analíticamente, incluso dentro de lo estrictamente académico, más aún si pensamos en problemas reales.
La enseñanza del cálculo numérico tiene una vertiente fundamental que es la experimentación. Sólo mediante ella se puede llegar a una compresión global del funcionamiento de los métodos, sobre todo cuando no es posible realizar un análisis teórico exhaustivo de los mismos (tampoco deseable en una formación que debe ser eminentemente práctica). De hecho, los grandes métodos se han gestado en la práctica y sus propiedades se han constatado experimentalmente antes de ser abordadas de forma teórica.
Desde el punto de vista pedagógico no podemos pretender que un alumno entienda la mecánica de un algoritmo sin utilizarlo en la práctica. La experimentación numérica, ya sea a mano o con calculadora, enmascara la utilidad de los métodos y los convierte en algo pesado y aburrido, perdiendo la agilidad que les debe caracterizar, por lo que solamente utilizando un equipo computacional de alguna potencia se puede dar mayor coherencia a su enseñanza.
La segunda vertiente básica del análisis numérico consiste en la implementación informática de los métodos, cosa que un alumno de primer curso universitario o de Bachillerato no está capacitado para hacer, al carecer de los conocimientos suficientes sobre lenguajes de programación. Sin embargo, hemos encontrado en los manipuladores simbólicos una herramienta de gran utilidad a la hora de que alumnos sin experiencia programadora en lenguajes avanzados experimenten con métodos numéricos simples. Por supuesto que la programación de métodos complicados presenta básicamente las mismas dificultades, si no más, que en un lenguaje de programación estándar como puede ser C/C++ o FORTRAN, siendo normalmente el código mucho más eficiente en estos últimos.
Debemos también indicar que el uso de un manipulador simbólico no se limita al cálculo numérico. Muchas otras ramas de la Matemática admiten la resolución de sus problemas mediante manipuladores. Por ejemplo, en geometría pueden ser especialmente útiles puesto que permiten representar gráficamente todo tipo de figuras de forma que el alumno puede visualizarlas y asociarlas a su ecuación fácilmente.
Resumiendo, creemos que, utilizado de forma adecuada, un manipulador simbólico puede constituir una herramienta inestimable para la enseñanza de las Matemáticas en el ámbito universitario. Además, contribuye a que las materias resulten más atractivas al alumno debido a que su relación con el ordenador es más activa, mientras que en las clases convencionales es muy difícil obtener su participación. Este hecho ha quedado patente en una encuesta realizada entre nuestros alumnos, los cuales no han dudado en calificar las prácticas realizadas con manipulador como interesantes y amenas en un alto porcentaje.
En la siguiente sección presentamos un ejemplo que ilustra la utilización del manipulador simbólico MAPLE V en la implementación y experimentación de algunos métodos numéricos sencillos. En él vemos como el programa permite un estudio del comportamiento del método en cuestión con suficiente profundidad y de forma rápida y sencilla, con escasos conocimientos de programación y pudiendo, además, obtener datos adicionales del problema sin dificultad.
Sin embargo, la manipulación simbólica transciende la enseñanza para constituir en la actualidad una herramienta imprescindible de muchos investigadores. De hecho, el origen de la manipulación simbólica hay que buscarlo precisamente en la investigación, rama en la que ha ahorrado mucho trabajo y esfuerzo a los científicos. En la última sección presentamos un ejemplo de aplicación a la investigación en Física Teórica.
Finalmente, queremos señalar que, aún cuando en esta comunicación nos hemos centrado en la manipulación simbólica, existen otras nuevas tecnologías que pueden mejorar el proceso educativo. Así, por ejemplo, creemos que Internet muestra múltiples posibilidades en cualquier materia y no nos referimos únicamente a ella como medio de obtener información sino, sobre todo, formación que es lo que debe interesar al educador.
En el siguiente ejemplo se presupone que el alumno tiene unos conocimientos básicos de MAPLE V y de los métodos numéricos empleados.
Tomando como punto de partida un problema que puede ser resuelto de forma tradicional, se motiva la experimentación numérica sobre el mismo, constatándose que la obtención de resultados con el manipulador es sencilla y rápida, aparte de permitir analizar los resultados de forma simultánea. Así mismo, las capacidades gráficas del programa posibilitan una mejor comprensión del comportamiento de los métodos estudiados.
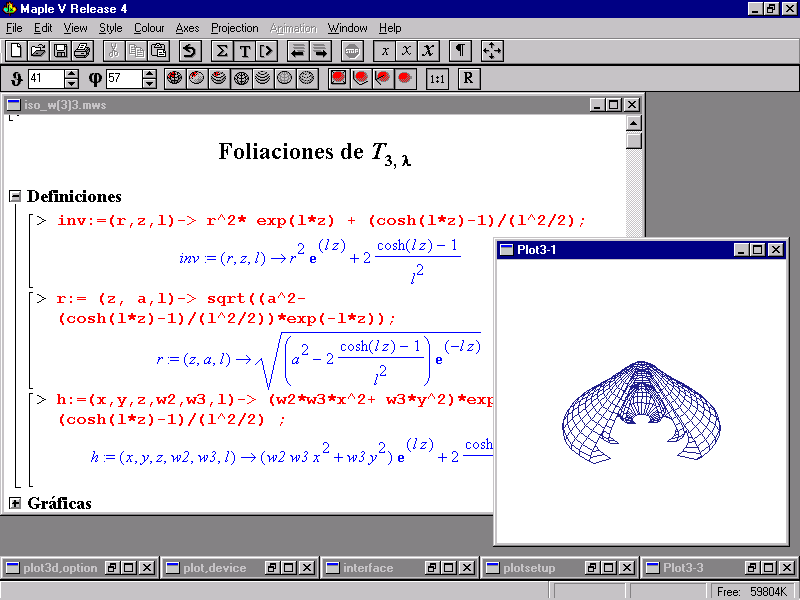
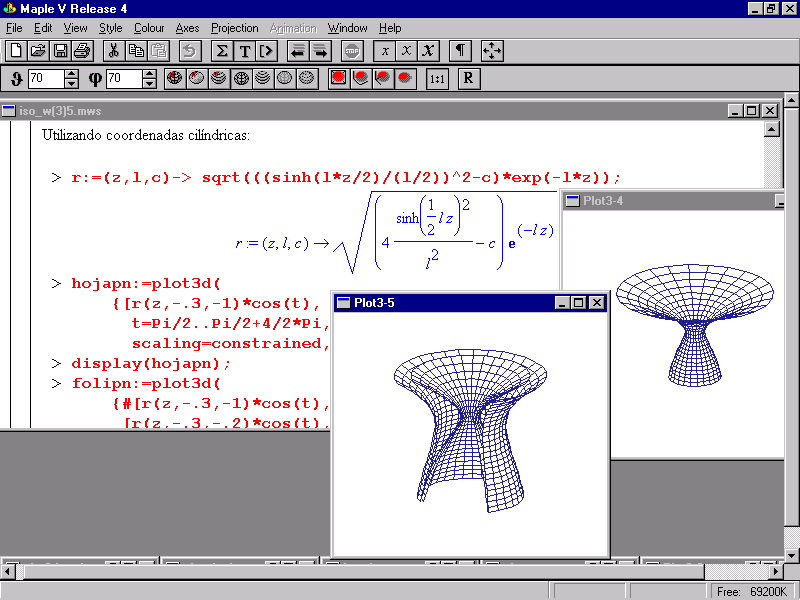
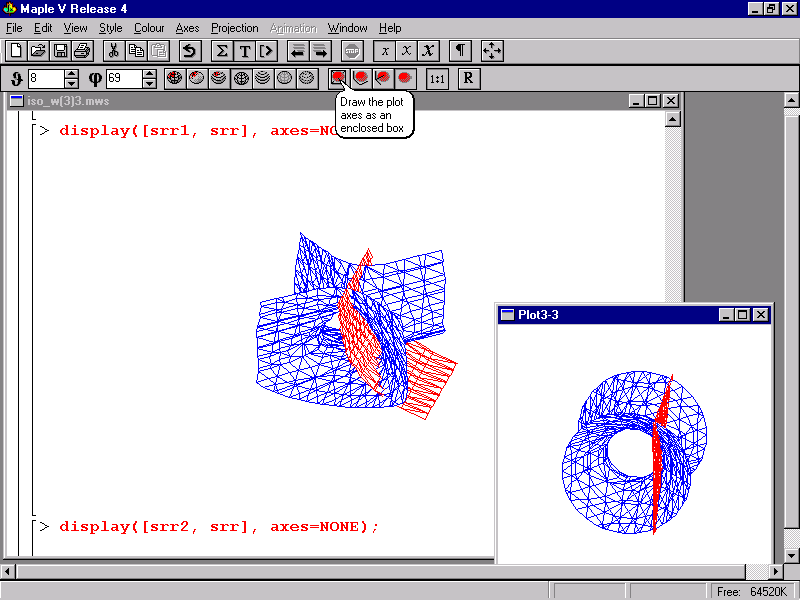
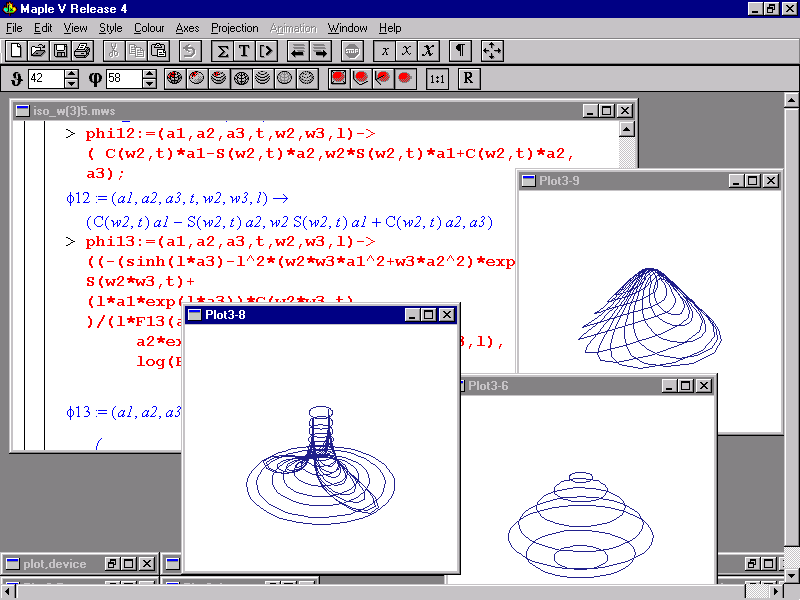
En las figuras que se acompañan mostramos una sesión de trabajo típica de una práctica interactiva, incluyendo algunos comentarios que muestran los aspectos didácticos más destacables.

Figura 1.
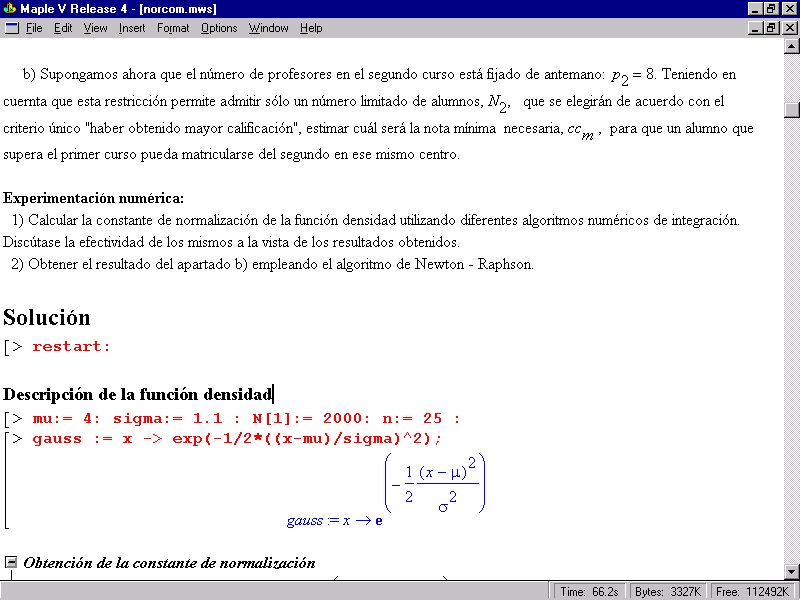
Figura 2.
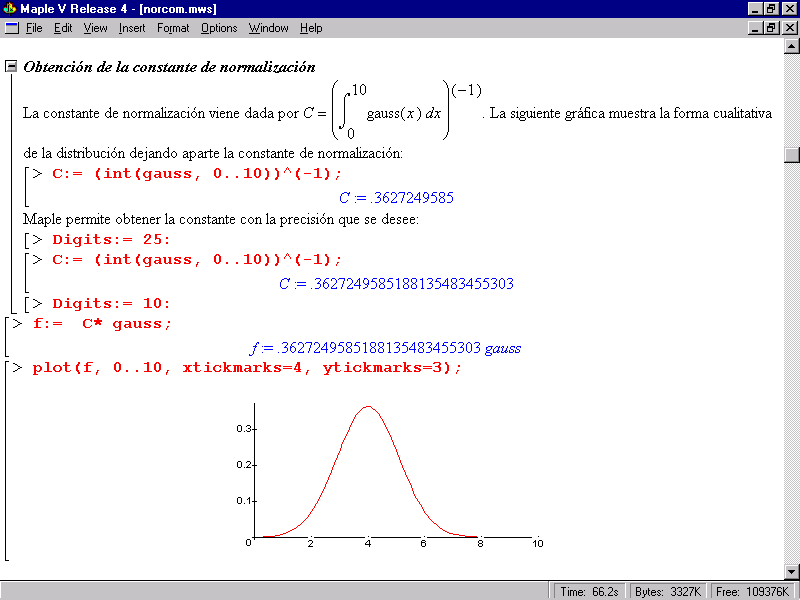
Figura 3.

Figura 4.
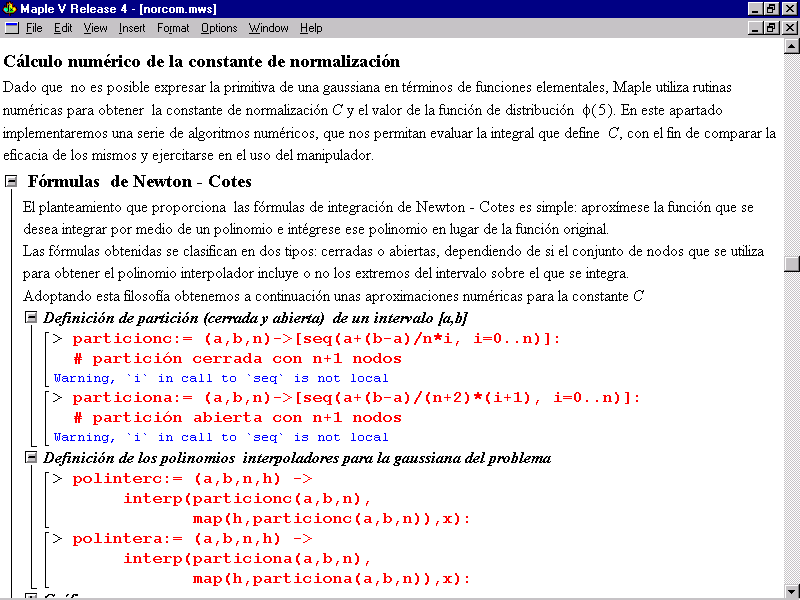
Figura 5.
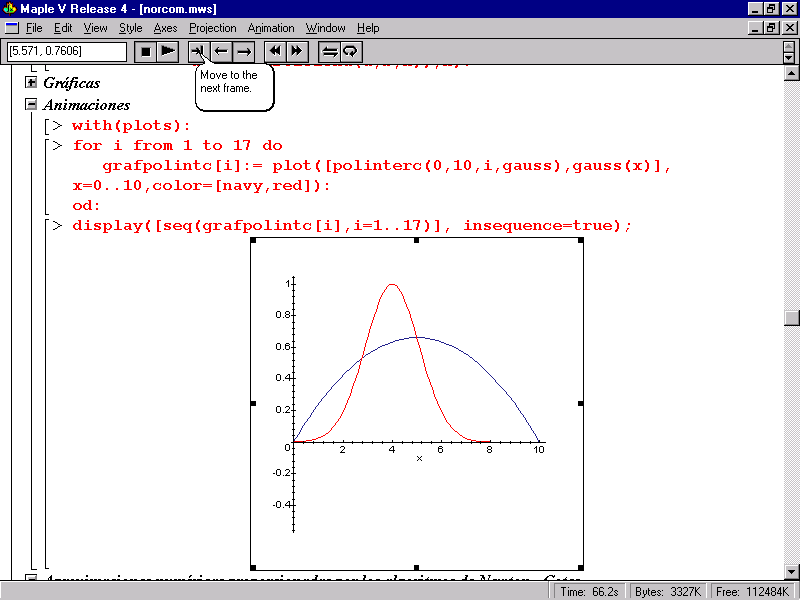
Figura 6.
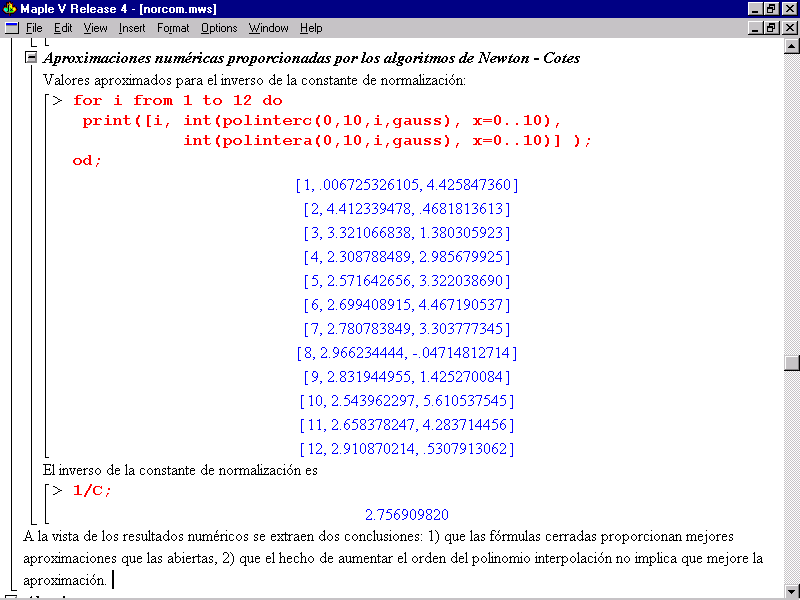
Figura 7.
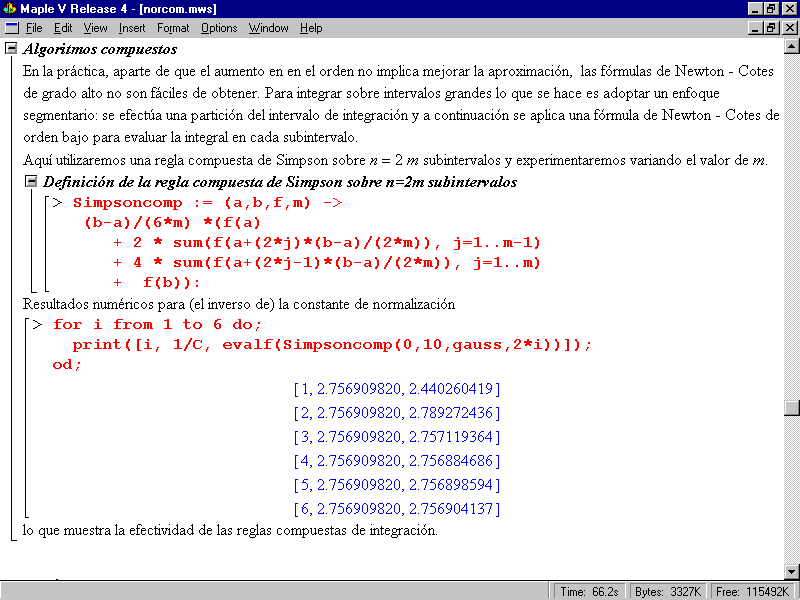
Figura 8.
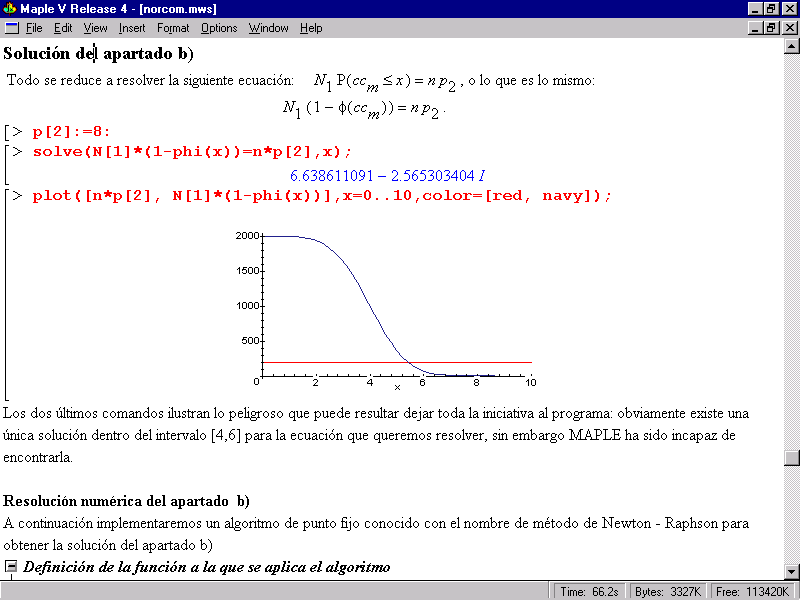
Figura 9.
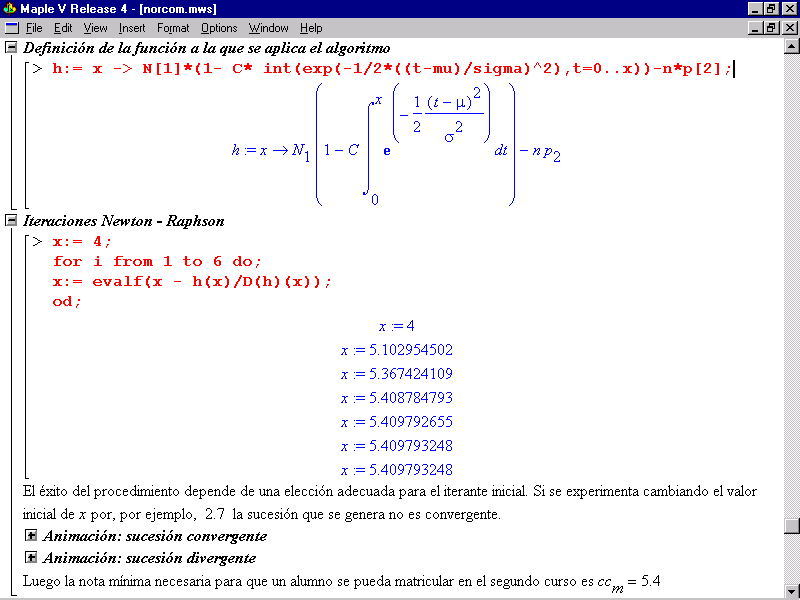
Figura 10.