Jaime Riera Guasp, Marcos H. Giménez Valentín, Ana Vidaurre y Isabel Salinas Marín.

En los últimos años se puede observar, en los distintos niveles de educación, un cambio desde la enseñanza centrada en la asignatura a un aprendizaje centrado en el estudiante. Este cambio en la filosofía y la práctica, se asocia a un cambio metodológico desde el instructivismo, basado en el diseño de tareas y recursos de aprendizaje utilizando un proceso deductivo y racional, al constructivismo (Duffy,1992).

En el ámbito universitario, la implantación de los nuevos Planes de Estudio, ofrece una oportunidad para que el profesor vaya cediendo parte de su protagonismo al alumno. En esa línea, se pretende orientarlo y motivarlo, así como proporcionarle información en una forma complementaria a la que aparece en los libros de texto. El desarrollo de estas ideas puede verse favorecido por la utilización de las Nuevas Tecnologías.

Riera (1997a) indica algunas de las técnicas que utilizamos: experiencias de aula, presentaciones multimedia, simulaciones digitales y digitalización de fenómenos. La implementación de estas técnicas se ha llevado a cabo en base a diferentes Proyectos de Innovación Educativa de la Universidad Politécnica de Valencia, aplicándolas en las asignaturas de Física de la E.U.I.T.I. La descripción de los procedimientos empleados y los resultados obtenidos han sido objeto de diferentes publicaciones (Riera, 1994; Vidaurre, 1994; Giménez, 1997a).

En la presente comunicación nos vamos a centrar en la simulación digital y en las distintas posibilidades que ofrece como apoyo a la docencia. A continuación se expondrá como ejemplo la aplicación que hacemos de esta técnica para facilitar la comprensión de uno de los temas en que hemos observado mayor dificultad de comprensión por parte de los alumnos: el de los procesos ondulatorios.

Muchos autores hacen referencia a las analogías como herramientas útiles para facilitar la comprensión de conceptos científicos. Los propios científicos las emplean a la hora de elaborar y presentar sus teorías (Wong, 1993). La tecnología ha tenido grandes éxitos con su uso, a través de las "simulaciones analógicas"; las maquetas y los modelos reducidos tienen gran prestigio en ingeniería.

La capacidad de cálculo e interactividad que ofrecían los ordenadores en las décadas precedentes posibilitaron la simulación numérica de todo tipo de procesos, por lo que se hicieron indispensables en la investigación científica. El desarrollo de los ordenadores multimedia, con su capacidad gráfica, de animación y sonido..., permite enriquecer dicha simulación: la simulación numérica y la analógica se integran, creando un nuevo "ambiente de aprendizaje" (De Corte,1992; Jones, 1992).

Tal y como ponen de manifiesto muchos autores (Wood, 1996), estos ambientes ofrecen una serie de ventajas, como la interactividad, la respuesta dinámica y la integración de medios, de las que no disponen otros más tradicionales. Además, en el ámbito universitario, habitualmente masificado, permiten una mayor personalización de la docencia. Por otro lado, la disponibilidad de equipos con la suficiente potencia es cada vez mayor, tanto merced a las aulas informáticas como en el propio domicilio de los alumnos.

Sin embargo, a pesar de que la tecnología básica para apoyar este desarrollo es muy poderosa hoy en día, los problemas de desarrollar sistemas de software de calidad que logren satisfactorios niveles de motivación, son todavía difíciles de resolver (Barker, 1997). De nuestro trabajo, que venimos desarrollando en este campo en los últimos años, hemos extraído algunas conclusiones acerca de características que deben tener los programas para alcanzar un mayor grado de eficacia. De forma resumida, podrían ser:

• Poseer un interfaz muy intuitivo.
• Simular procesos físicos relativamente complejos.
• Proporcionar referencias visuales del proceso a través de animaciones.

De acuerdo con estos requisitos hemos desarrollado un paquete informático (Riera, 1997b) que simula procesos tales como la traslación y rotación de sólidos rígidos, la composición de movimientos vibratorios y los sistemas oscilantes. Giménez (1997b, 1998) y Riera (1997c) describen la forma de integrar este tipo de programas en la dinámica del curso, apoyando tanto a las clases de teoría como a las experiencias de aula y al experimento.

Uno de los temas en que hemos observado una mayor dificultad para asimilar los conceptos por parte de los alumnos, es el de los procesos ondulatorios. Por su misma esencia, requieren una visualización tanto en el espacio como en el tiempo, por lo que resulta complejo representar los conceptos implicados mediante imágenes estáticas. Por otra parte, las experiencias de aula, aunque muy útiles, no permiten fácilmente aislar los aspectos que se quieren enfatizar en cada caso, ni tampoco controlar la magnitud de las variables implicadas. Además, hemos podido observar que tanto las imágenes estáticas como las experiencias de aula resultan inadecuadas para la observación de algunos tipos de ondas, como las longitudinales, y de algunos conceptos, como la velocidad.

En consecuencia, los procesos ondulatorios suponen un campo muy adecuado para la utilización de la simulación digital: son relativamente complejos, y la animación por ordenador puede resultar clarificadora y versátil.

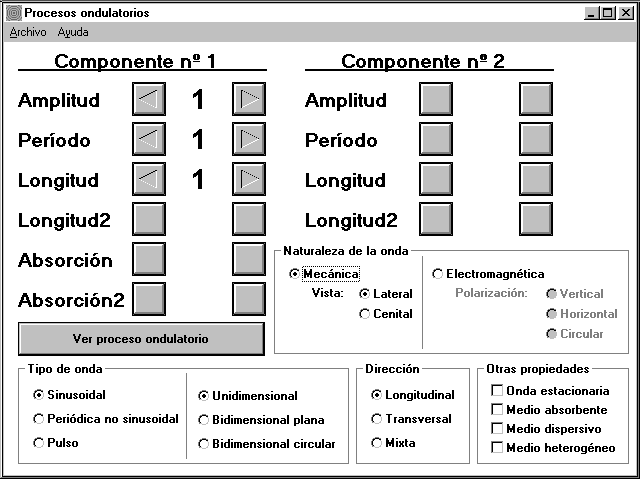
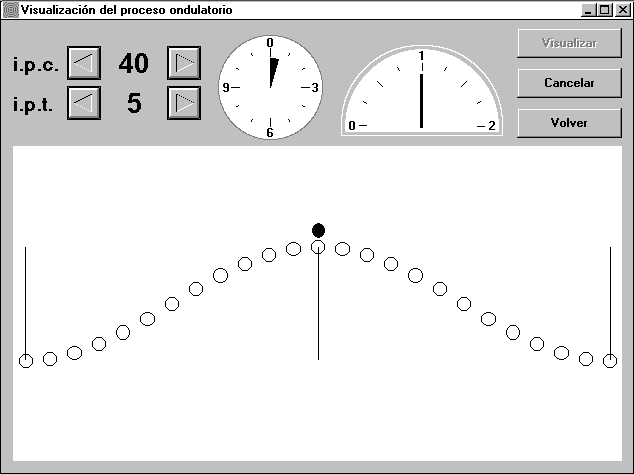
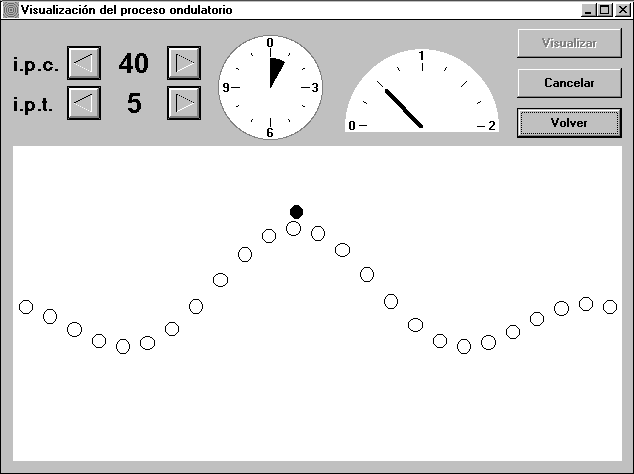
El programa ONDAS, realizado en Visual Basic, consta de dos pantallas: la principal (Fig. 1), donde se seleccionan las opciones y los valores de las variables; y la de visualización (Fig. 2), donde se muestra mediante animación el proceso ondulatorio con las características elegidas. A continuación se describe esta segunda pantalla, quedando para el próximo apartado la relación detallada de las diversas opciones que ofrece la pantalla principal.

Como se observa en la Fig. 2, la onda se pone de manifiesto por la forma en que afecta a una serie de osciladores individuales representados por circunferencias. Es posible hacer visible la trayectoria de cualquiera de esos osciladores, como es el caso de los situados a la izquierda, a la derecha y en el centro en la Fig. 2. También se puede ver un círculo situado sobre la cresta de la onda, y que se mueve con ella. Esto permite diferenciar el movimiento y velocidad de la onda, representados por dicho círculo, del movimiento y velocidad de los osciladores individuales.

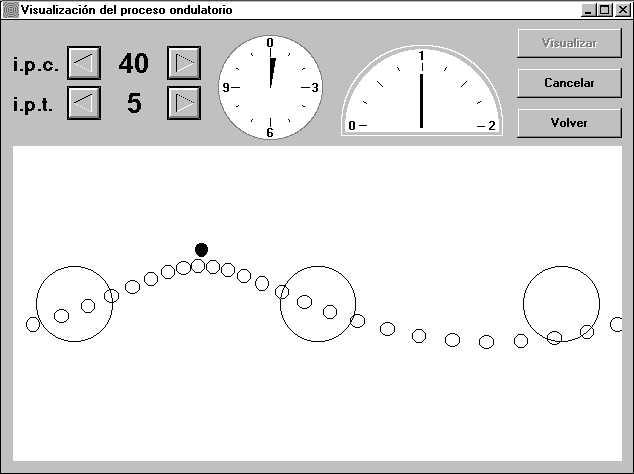
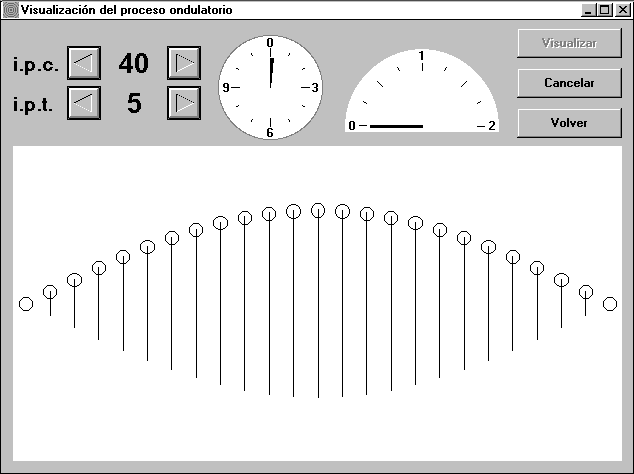
La Fig. 2 muestra una onda transversal, pero el programa permite también observar la animación de una onda longitudinal, difícil de percibir en una imagen estática, e incluso la de una onda mixta, como es el caso del oleaje. La Fig. 3 muestra esta onda mixta, así como las trayectorias seguidas por tres de los osciladores individuales afectados por la misma.

En la parte superior de la pantalla de visualización aparecen dos indicadores:

- El indicador circular es un cronómetro que se pone a cero al transcurrir un período de la onda. Entre sus utilidades está la de comprobar que dicho período coincide con el de todos los osciladores individuales.

- El indicador semicircular es un velocímetro que indica la velocidad de la onda. Entre sus utilidades está la de cuantificar la variación de dicha velocidad cuando el medio es heterogéneo.

En las Figs. 2 y 3 se muestran ondas progresivas sinusoidales en un medio homogéneo no dispersivo ni absorbente. Sin embargo, son posibles muchas más combinaciones, seleccionables desde la pantalla principal del programa, tal y como se describe seguidamente.

Con carácter general, la pantalla principal del programa ONDAS permite asignar valores a la amplitud, el período y la longitud de la onda. Estas variables son suficientes en una gran cantidad de casos. Sin embargo, en otros, relacionados con las diferentes opciones que se describen posteriormente, se activan otras variables adicionales: la amplitud y el período de una segunda componente de la onda (para ondas periódicas no sinusoidales), una segunda longitud de onda (para medios heterogéneos, con un cambio en la velocidad de la onda), y coeficientes de absorción (para medios absorbentes).

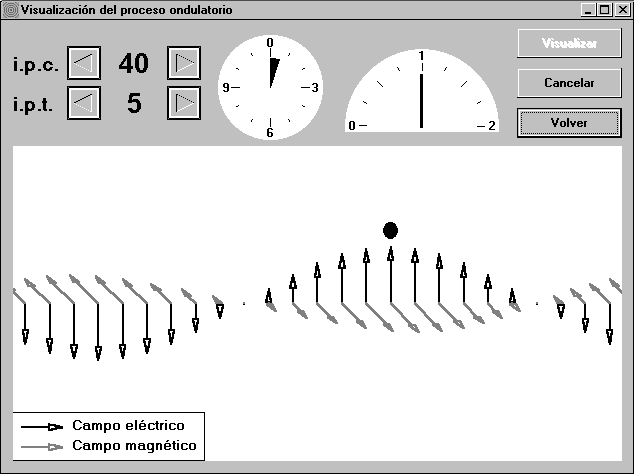
- Naturaleza de la onda. Se puede elegir si la onda es mecánica o electromagnética. En el caso de una onda mecánica, la animación muestra cómo dicha onda afecta a los osciladores individuales, bien desde un punto de vista lateral como el mostrado en las Figs. 2 y 3, bien como una vista cenital, donde la oscilación transversal aparenta ser perpendicular a la pantalla. Por otro lado, la onda electromagnética se pone de manifiesto, no con partículas móviles, sino con los vectores campo eléctrico y magnético, tal y como se muestra en la Fig. 4. En dicha figura se visualiza una onda polarizada verticalmente, pero también se permite optar por una polarización horizontal o circular.

- Dirección. Si la onda es mecánica, se puede optar por que sea transversal, longitudinal o mixta. En el caso de esta última, las componentes longitudinal y transversal son de igual amplitud y están en cuadratura, como corresponde al caso de las ondas superficiales de gravedad en aguas profundas.

- Tipo de onda (I). El primer conjunto de opciones es el de sinusoidal, periódica no sinusoidal y pulso. Las Figs. 2, 3 y 4 corresponden a ondas sinusoidales, caracterizadas por una amplitud, un período y una longitud. La Fig. 5 muestra una onda periódica no sinusoidal, caso en el que el programa permite asignar valores a la amplitud y el período de una segunda componente sinusoidal. El programa selecciona automáticamente la longitud de onda para que ambas componentes tengan la misma velocidad, salvo que se active la opción, descrita más adelante, por la que el medio pasa a ser dispersivo. También es posible optar por un pulso, caracterizado por su amplitud, su duración y su longitud.

- Tipo de onda (II). Permite seleccionar entre una onda longitudinal, como las mostradas hasta ahora, una bidimensional plana, o una bidimensional circular.

- Onda estacionaria. Si se activa esta opción, a la onda progresiva que viaja de izquierda a derecha se le superpone otra igual pero de sentido contrario. La Fig. 6 muestra un ejemplo para el caso de una onda sinusoidal transversal cuya longitud de onda es el doble de la pantalla. Se ha activado la visualización de las trayectorias de todos los osciladores individuales para poner de manifiesto la presencia de los nodos y del antinodo.

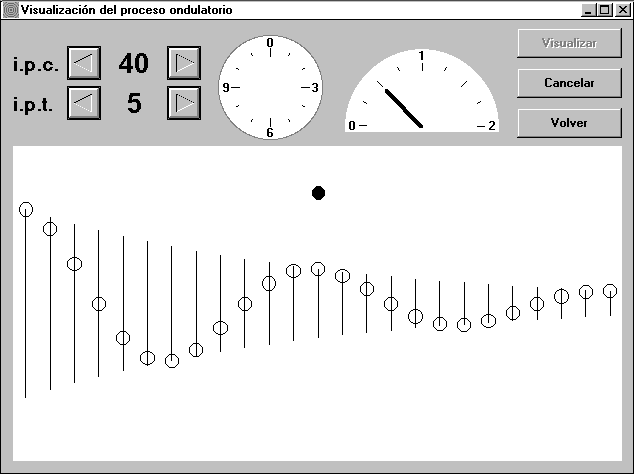
- Medio absorbente. Cuando esta opción está activa, es posible asignar un valor (dos si además el medio es heterogéneo) al coeficiente de absorción. La Fig. 7 representa un ejemplo que corresponde a una onda transversal. Las trayectorias de los distintos osciladores muestran cómo se reduce la amplitud con la distancia.

- Medio dispersivo. Si la onda es periódica no sinusoidal, se asigna a la segunda componente una velocidad distinta que a la primera. En concreto, la velocidad de cada componente sinusoidal varía con la raíz cuadrada de su longitud de onda. Esta relación corresponde a las ondas superficiales de gravedad en aguas profundas.

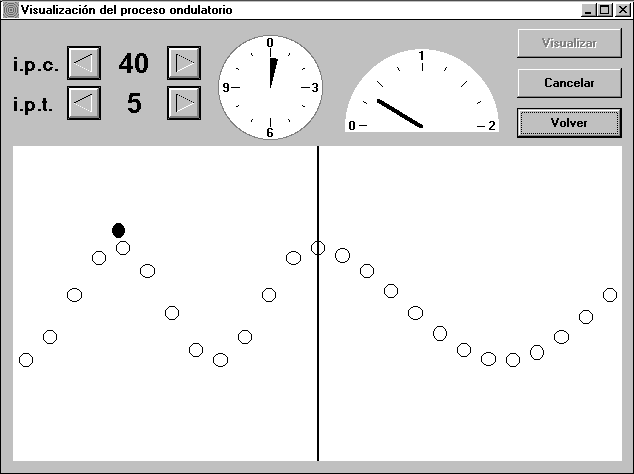
- Medio heterogéneo. Cuando se activa esta opción, la pantalla principal permite asignar dos valores a la longitud de onda. La pantalla de visualización queda dividida en dos mitades, cada una de las cuales tiene asignada una de esas longitudes de onda. La Fig. 8 muestra el resultado para una onda sinusoidal transversal donde la longitud de onda en la parte derecha es el doble que en la izquierda. Puede así comprobarse que ese cambio no es perceptible al observar un oscilador individual, pero sí en la forma de la onda. También se pone de manifiesto que al cambiar de medio, la velocidad de la onda se duplica.

Se pueden seleccionar múltiples combinaciones de las opciones indicadas. Por ejemplo, es posible visualizar una onda transversal estacionaria no sinusoidal en un medio dispersivo y heterogéneo.

De la descripción hecha de las opciones del programa ONDAS se deduce una gran cantidad de aplicaciones que permiten visualizar mediante las animaciones diferentes aspectos de los procesos ondulatorios que resultan en general de difícil comprensión por parte de los alumnos (ondas longitudinales y mixtas, cambios en la velocidad de la onda, ...). En este apartado se sugieren algunas aplicaciones menos obvias pero de gran interés:

- A partir de la animación que corresponde a la Fig. 2, puede comprobarse que mientras el oscilador situado a la izquierda (o cualquier otro) completa un ciclo de su movimiento, el círculo situado sobre la cresta recorre la longitud de onda. Queda así demostrado de una forma gráfica que la longitud de la onda es igual a su velocidad por el período.

- Se puede observar una onda estacionaria sinusoidal. A continuación se añade una segunda componente con, por ejemplo, la mitad de período, y variar su amplitud para observar los resultados. Se simula así el efecto de la superposición de un sobretono a una frecuencia fundamental.

- Al visualizar una onda no sinusoidal en un medio no dispersivo, se observa una forma de onda constante que se traslada a una velocidad determinada. Si a continuación se activa la opción de medio dispersivo, la forma de onda ya no se conserva.

- Cuando se tiene una onda mixta no sinusoidal, las trayectorias descritas por los osciladores individuales son curvas cerradas de formas peculiares, aunque iguales. Las formas de estas trayectorias son incluso más llamativas cuando el medio es dispersivo.

Barker, P.G. (1997). "Enhancing learning opportunities through electronic course delivery". Creación de Materiales para la Innovación Educativa con Nuevas Tecnologías, EDUTEC'97, Málaga.

De Corte, E., Linn, M., Mandl, H., Verchaffel, L. (1992). "Computer-Based Learning Environments and Problem Solving". Springer-Verlag. Berlín

Duffy, T., Jonassen, D. (1992). "Constructivism and the technology of instruction".LEA.

Giménez, M.H., Vidaurre, A. y Riera, J. (1997a). "Simulación de procesos físicos con tecnología multimedia". V Congreso Internacional sobre la Investigación Didáctica de las Ciencias. Murcia. 85-86.

Giménez, M.H., Riera, J. y Vidaurre, A. (1997b). "Simulación analógica y digital de la composición de vibraciones armónicas". V Congreso Universitario sobre Innovación Metodológica en las Enseñanzas Técnicas, Barcelona, 369-376.

Giménez, M.H., Riera, J. y Vidaurre, A. (1998). "Analogical and digital simulation of mechanical and electrical oscillators". Experiments and Measurements in Engineering Physics Education, EMEPE'98, Brno, Czech Republic, 115-118.

Jones, M., Winne, P., (1992). "Adaptive learning environments: foundations and frontiers". Springer Verag. Berlín.

Riera, J., Vidaurre, A. y Giménez, M.H. (1994). "La evaluación continua como técnica motivadora en el proceso de enseñanza". II Congreso Sobre Reforma Planes Estudio, Cádiz.

Riera, J., Giménez, M.H. y Vidaurre, A. (1997a). "Hacia la utilización de técnicas multimedia en el aula. Una aproximación a la enseñanza de la Física en la E.U.I.T.I. de Valencia". Creación de Materiales para la Innovación Educativa con Nuevas Tecnologías, EDUTEC'97, Málaga, 630-634.

Riera, J., Vidaurre, A. y Giménez, M.H. (1997b). Programas de simulación de procesos físicos. Universidad Politécnica de Valencia, SPUPV-97.148.

Riera, J., Vidaurre, A., Giménez, M.H. y Torregrosa, C. (1997c). "Rotation dinamics by digital simulation". Physics Teaching in Engineering Education. Copenhagen, Denmark.

Vidaurre, A., Giménez, M.H. y Riera, J. (1994). "La evaluación continua como técnica motivadora en el proceso de enseñanza. Continuación de una experiencia". II Jornadas sobre la Innovación Docente en las Escuelas Técnicas Universitarias, Valencia.

Wong, E.D., (1993). "Self-generated analogies as a tool for constructing and evaluating explanations of scientific phenomena". Journal of Research in ScienceTeaching, 30(4), 367-380 .

Wood, S.L. (1996). "A new approach to interactive tutorial software for engineering education". IEEE Transactions on Eductation, 39(3), 399-408.